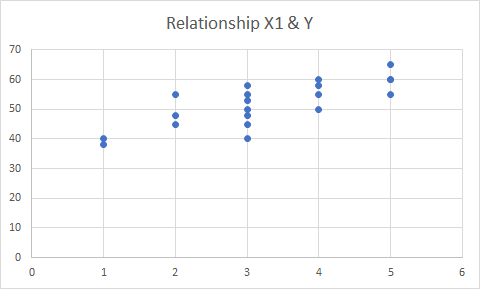
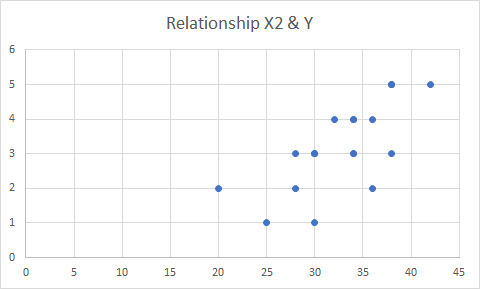
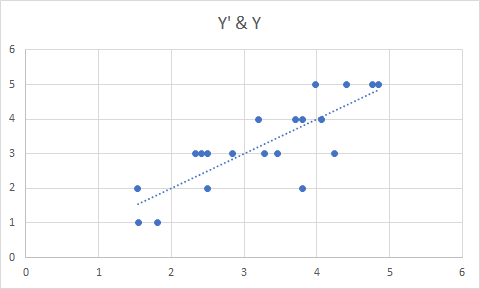
Plotly.py 3.0.0 was recently released, and I finally got a chance to tinker with it! This is exciting because this release includes features that are specifically designed for Jupyter Notebooks. Namely, JavaScript is directly embedded in the figure that you can now access directly through your notebook. Exciting!
If you haven’t installed plotly or need to upgrade, open your Anaconda command prompt (as Administrator) and follow these directions. After you install plotly, launch Jupyter Notebook (by typing “Jupyter Notebook” into your Anaconda command prompt or by opening Jupyter Notebook using your computer menu). Next, enter your plotly username and api key in your notebook. You can sign up for plotly here. Directions for generating an api key here.
#first import plotly and provide username and api key
import plotly
plotly.tools.set_credentials_file(username='UserName', api_key='XXXXX')
Now load the following:
import plotly.plotly as py
import plotly.graph_objs as go
from plotly.offline import download_plotlyjs, init_notebook_mode, plot, iplot
import numpy as np
import pandas as pd
init_notebook_mode(connected=True) #tells the notebook to load figures in offline mode
Plotly should now work within your notebook.
Here’s an example of a 2D plot:
x=np.random.randn(1000)
y=np.random.randn(1000)
go.FigureWidget(
data=[
{'x': x, 'y': y, 'type': 'histogram2dcontour'}
]
)
 Example of a 2D plot with markers:
Example of a 2D plot with markers:
x = np.random.randn(2000)
y = np.random.randn(2000)
iplot([go.Histogram2dContour(x=x, y=y, contours=dict(coloring='heatmap')),
go.Scatter(x=x, y=y, mode='markers', marker=dict(color='white', size=3, opacity=0.3))], show_link=False)
 Example of a 3D plot:
Example of a 3D plot:
s = np.linspace(0, 2 * np.pi, 240)
t = np.linspace(0, np.pi, 240)
tGrid, sGrid = np.meshgrid(s, t)
r = 2 + np.sin(7 * sGrid + 5 * tGrid) # r = 2 + sin(7s+5t)
x = r * np.cos(sGrid) * np.sin(tGrid) # x = r*cos(s)*sin(t)
y = r * np.sin(sGrid) * np.sin(tGrid) # y = r*sin(s)*sin(t)
z = r * np.cos(tGrid) # z = r*cos(t)
surface = go.Surface(x=x, y=y, z=z)
data = [surface]
layout = go.Layout(
title='Parametric Plot',
scene=dict(
xaxis=dict(
gridcolor='rgb(255, 255, 255)',
zerolinecolor='rgb(255, 255, 255)',
showbackground=True,
backgroundcolor='rgb(230, 230,230)'
),
yaxis=dict(
gridcolor='rgb(255, 255, 255)',
zerolinecolor='rgb(255, 255, 255)',
showbackground=True,
backgroundcolor='rgb(230, 230,230)'
),
zaxis=dict(
gridcolor='rgb(255, 255, 255)',
zerolinecolor='rgb(255, 255, 255)',
showbackground=True,
backgroundcolor='rgb(230, 230,230)'
)
)
)
fig = go.Figure(data=data, layout=layout)
py.iplot(fig, filename='jupyter-parametric_plot')

Lastly, an animated plot:
from plotly.offline import init_notebook_mode, iplot
from IPython.display import display, HTML
init_notebook_mode(connected=True)
url = 'https://raw.githubusercontent.com/plotly/datasets/master/gapminderDataFiveYear.csv'
dataset = pd.read_csv(url)
years = ['1952', '1962', '1967', '1972', '1977', '1982', '1987', '1992', '1997', '2002', '2007']
# make list of continents
continents = []
for continent in dataset['continent']:
if continent not in continents:
continents.append(continent)
# make figure
figure = {
'data': [],
'layout': {},
'frames': []
}
# fill in most of layout
figure['layout']['xaxis'] = {'range': [30, 85], 'title': 'Life Expectancy'}
figure['layout']['yaxis'] = {'title': 'GDP per Capita', 'type': 'log'}
figure['layout']['hovermode'] = 'closest'
figure['layout']['sliders'] = {
'args': [
'transition', {
'duration': 400,
'easing': 'cubic-in-out'
}
],
'initialValue': '1952',
'plotlycommand': 'animate',
'values': years,
'visible': True
}
figure['layout']['updatemenus'] = [
{
'buttons': [
{
'args': [None, {'frame': {'duration': 500, 'redraw': False},
'fromcurrent': True, 'transition': {'duration': 300, 'easing': 'quadratic-in-out'}}],
'label': 'Play',
'method': 'animate'
},
{
'args': [[None], {'frame': {'duration': 0, 'redraw': False}, 'mode': 'immediate',
'transition': {'duration': 0}}],
'label': 'Pause',
'method': 'animate'
}
],
'direction': 'left',
'pad': {'r': 10, 't': 87},
'showactive': False,
'type': 'buttons',
'x': 0.1,
'xanchor': 'right',
'y': 0,
'yanchor': 'top'
}
]
#custom colors
custom_colors = {
'Asia': 'rgb(171, 99, 250)',
'Europe': 'rgb(230, 99, 250)',
'Africa': 'rgb(99, 110, 250)',
'Americas': 'rgb(25, 211, 243)',
'Oceania': 'rgb(50, 170, 255)'
}
sliders_dict = {
'active': 0,
'yanchor': 'top',
'xanchor': 'left',
'currentvalue': {
'font': {'size': 20},
'prefix': 'Year:',
'visible': True,
'xanchor': 'right'
},
'transition': {'duration': 300, 'easing': 'cubic-in-out'},
'pad': {'b': 10, 't': 50},
'len': 0.9,
'x': 0.1,
'y': 0,
'steps': []
}
# make data
year = 1952
for continent in continents:
dataset_by_year = dataset[dataset['year'] == year]
dataset_by_year_and_cont = dataset_by_year[dataset_by_year['continent'] == continent]
data_dict = {
'x': list(dataset_by_year_and_cont['lifeExp']),
'y': list(dataset_by_year_and_cont['gdpPercap']),
'mode': 'markers',
'text': list(dataset_by_year_and_cont['country']),
'marker': {
'sizemode': 'area',
'sizeref': 200000,
'size': list(dataset_by_year_and_cont['pop'])
},
'name': continent
}
figure['data'].append(data_dict)
# make frames
for year in years:
frame = {'data': [], 'name': str(year)}
for continent in continents:
dataset_by_year = dataset[dataset['year'] == int(year)]
dataset_by_year_and_cont = dataset_by_year[dataset_by_year['continent'] == continent]
data_dict = {
'x': list(dataset_by_year_and_cont['lifeExp']),
'y': list(dataset_by_year_and_cont['gdpPercap']),
'mode': 'markers',
'text': list(dataset_by_year_and_cont['country']),
'marker': {
'sizemode': 'area',
'sizeref': 200000,
'size': list(dataset_by_year_and_cont['pop'])
},
'name': continent
}
frame['data'].append(data_dict)
figure['frames'].append(frame)
slider_step = {'args': [
[year],
{'frame': {'duration': 300, 'redraw': False},
'mode': 'immediate',
'transition': {'duration': 300}}
],
'label': year,
'method': 'animate'}
sliders_dict['steps'].append(slider_step)
figure['layout']['sliders'] = [sliders_dict]
iplot(figure)

Neat, right?!
Overall, everything ran smoothly except the last plot. I actually initially tried to make this one:
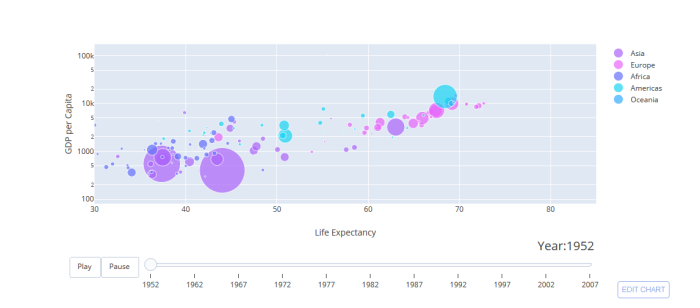
but I kept getting an error:
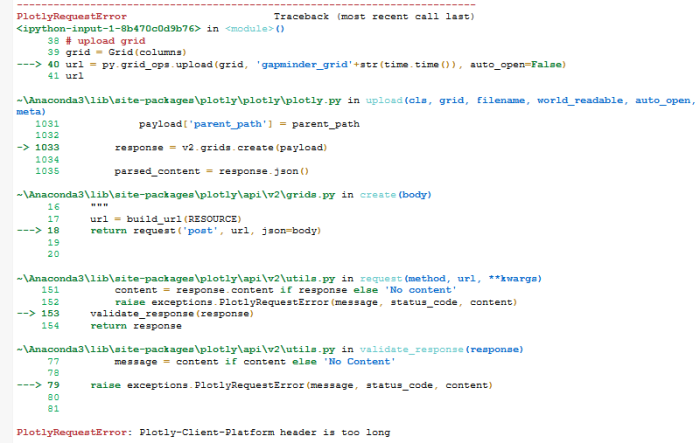
Update: Jon commented and pointed out that I was using an older version of plotly (3.0.0rc10) instead of 3.0.0rc11. You can check which version you have by typing the following:
import plotly
plotly.__version__
After I updated plotly, I successfully made the last graph!
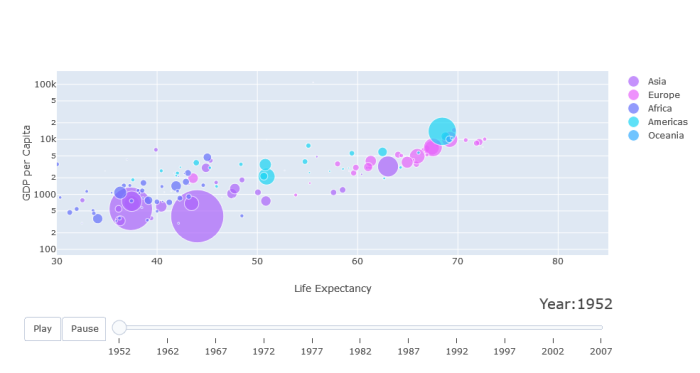
Special thanks to Jon! I sincerely appreciate your help!